Mathe-match-ics
By Matt Baker - Wednesday, February 10, 2021

In this post I’ll teach a two-deck version of Alex Elmsley’s brilliant routine “Arith-mate-ic” and explain the nuts and bolts of why it works. Towards the end, I’ll throw in some bonus ideas which should be of interest to memorized deck practitioners.
The Effect
On the table are two decks of cards, one red-backed and the other blue. The magician shuffles the red deck while saying, “Many of the great thinkers who write about the art of magic have tried to define what magic is, exactly. It’s not easy to do, as it turns out — there’s really no one definition which encompasses the full texture of our art. However, one of the definitions I’m fond of is that magic is the skillful elevation of coincidence to certainty.”
The red deck is handed to a participant face-down. “Your job is to predict an unlikely coincidence, and mine is to make your improbable conjecture come true. You’ll choose a random number by cutting off some cards from the pack, and that number will be your prediction. The only restriction is that — to keep this from getting too long — you should cut off less than half the deck.”
The participant cuts off a packet as instructed. The magician spreads the cut-off packet face-down on the table and cleanly and clearly counts the cards one by one. Let’s assume that the spectator has cut off 17 cards.
“17, very good. Now it’s up to me to manufacture a coincidence.” The magician takes the blue deck and cuts off a small packet, which is set aside. The remaining portions of the blue and red decks are placed side by side.
The magician turns over the top card of each remaining portion, laying the two cards face-up in front of their respective decks. They are not the same card. “Had these cards matched, that would have been quite a coincidence. But not a prognosticated one. You predicted the number 17, and if I’ve been successful the coincidence will take place precisely when we reach the 17th card in each deck — no more and no less.”
The magician continues simultaneously turning over the top cards of the two face-down piles, counting aloud as each pair is flipped onto the respective face-up packets. None of the pairs is a match. However, when the magician reaches the spectator’s predicted number, the 17th cards are flipped over… and they are exactly the same card.
A True Story
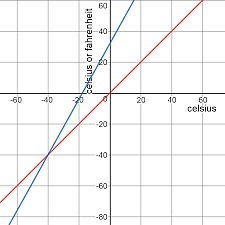
The only time I was ever thrown out of a classroom was in AP English during my senior year of high school. We were reading Alexander Solzhenitsyn’s decidedly unfunny novel entitled “One Day in the Life of Ivan Denisovich”, which is set in a Soviet labor camp in Siberia. At one point, Solzhenitsyn mentions that the temperature outside was minus 40. My friend Josh and I (who were co-captains of our high School’s math team) simultaneously blurted out, “Is that Fahrenheit or Celsius?” and then began laughing uncontrollably. The teacher, looking a bit shocked and not at all amused, demanded that we leave the classroom.
Explaining the Joke
What, you might ask, were we laughing at? Well, Josh and I both happened to know that minus 40 is the unique temperature at which the Fahrenheit and Celsius scales agree. And because we were unbelievable nerds, we found this hilarious (despite the fact that we were reading a book about a gulag).
Explaining the Trick
And what, you might also ask, does this have to do with the Alex Elmsley trick? A lot, as it turns out: Elmsley’s trick also boils down to determining the unique point at which two straight lines meet.
Let me explain. First of all, both decks are secretly stacked (and the red deck is given a false shuffle). And the magician always cuts the blue deck to the same (crimped) card. With these bits of subterfuge out of the way, we can get down to analyzing the core mathematics underpinning the effect.
The idea is simply this: the blue deck has a stack (it can be any stack that looks random) of 26 cards on top, and the red deck has the same 26-card stack, in the same order, but spaced out by twos. This can be achieved most rapidly by first arranging the red deck so that the top 26 cards are the same as those in the blue deck, and then giving the red deck a perfect in-faro shuffle.
The key point is that once the participant cuts off a packet of red cards and counts them — let’s say there are N cards in her packet — and the blue deck is cut to the crimp (bringing the stack to the top), the red stack starts N cards ahead of the blue stack. However, because the red stack has been spaced out by twos but the blue stack has not, we run through the cards in the blue stack twice as fast as those in the red stack.
So, when will the first coincidence occur? It’s easy enough to figure out using algebra, but it’s probably more intuitive to think of it as follows. Imagine that a red tortoise and a blue hare are racing, and that the hare runs exactly twice as fast as the tortoise (yes, I know, it’s either a very slow hare or a very fast tortoise). To compensate for his slowness, the tortoise starts N meters ahead of the hare. When will the hare catch up with the tortoise? It shouldn’t be hard to convince yourself that the hare will pass the tortoise after the tortoise has traveled exactly N meters further (because at that moment, the the hare will have traveled 2N meters, precisely wiping out the tortoise’s head start).
Here’s a graph representing the situation with N=17
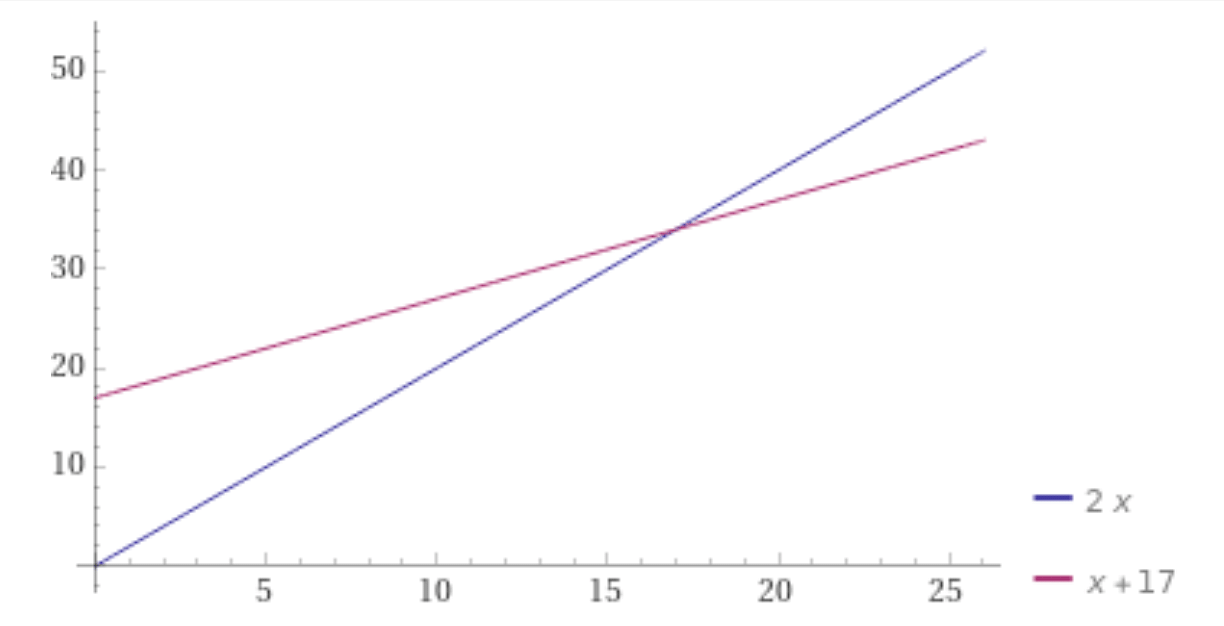
Algebraically, we’re simply saying that the lines y=2x and y=x+17 intersect when 2x=x+17, which happens precisely when x=17.
Back to the Elmsley effect: well, it’s the same thing! Suppose that on top of the blue deck we have cards labeled 1,2,…,26 (a bottom-cutting reverse breather crimp in card #52 will bring us to this situation with a single cut). The red deck will then be in the following order: *,1,*,2,*,3,…,*,26 (where * means any card not belonging to the 26-card stack). If you cut a packet of N cards off the red deck and then deal cards from the two decks simultaneously, as in the Elmsley trick, the first coincidence will occur on the Nth card. For example, if N=4 then we’ve cut off *,1,*,2 and the red deck will continue *,3,*,4,*,5,… while the blue deck will be 1,2,3,4,5,6,… In this case we see explicitly that the first coincidence will occur on the 4th card.
Summary
Before the trick begins, do the following:
Arrange a half-stack on top of the blue deck and put a bottom-cutting reverse breather crimp into the bottom card of the deck. Cut the blue deck so that the breather is about a third of the way down.
Arrange the red deck so that the top 26 cards are the same as the half-stack in the blue deck. Now give the red deck a perfect in-shuffle.
You’re ready to perform the trick.

Routined Mathe-match-ics
Denis Behr had the terrific idea to turn Alex Elmsley’s original (single-deck) “Arith-mate-ic” trick into a three-phase routine where the effect is repeated two more times under increasingly stringent conditions. You can (and should!) do the same thing with the two-deck routine described here. Denis’s insight was that by simply changing the relative order in which the spectator’s cut, the magician’s cut, and the counting of the spectator’s cards occur, you can make it feel like the conditions are becoming increasingly more stringent even though you actually do exactly the same thing three times in a row! While the method doesn’t change from one phase to another, the participant’s perception of what’s happening does, because it seems like the magician must somehow be adjusting his/her cuts according to how many cards the spectator cut off. For further details, see Denis’s “Routined Arith-mate-ic” (credits below).
Bonus Routine for Memdeck Users
If you use a memorized deck — it doesn’t matter which stack — you can get into the setup required for “Mathe-match-ics” with a single in-faro, starting from two decks in stack order. At the end of the trick, the blue deck will still be in stack order and the red deck will be just an anti-faro away. Here’s a little routine you can use to get back to the initial state where both decks are in their original stack order.
Give the blue deck a false shuffle followed by a genuine cut, noting the stack number of the bottom (face) card of the deck. Now do a cross-cut force to force the next card in your stack on a participant. However, for purposes of time misdirection, don’t reveal the (forced) selection just yet — leave one half criss-crossed on top of the other half, saying that you’ll get back to this deck in a bit.
Give the red deck a false shuffle and/or false cut. Say that you will rapidly memorize the red deck using a “binary mental sorting procedure” that you’ve been working on. Having said this, you can openly do an in-the-hands anti-faro by running through the faces of the cards and up-jogging every other one, starting with the top card. Pretend to concentrate as you’re doing this, even though you’ll probably feel like laughing instead. When you’ve finished running through the cards, gaze up at the sky for a moment as if to complete some mental calculations and then confidently announce, “Got it!” Casually strip out the up-jogged cards and place them onto the face of the remaining cards. Now turn the red deck face-down, place it into its case, and hand it to a spectator.
Now come back to the blue deck. Have your participant remove the card she “cut to”. Announce that you’ll try to figure out which card is missing by looking through the remaining cards. Explain that this is a bit easier than memorizing the order of every single card as you did with the red deck. Spread the blue deck face-up, rapidly scan the faces, and then close the spread and place the blue deck face-down again. Announce the selection (whose stack number you know is one more than the card you glimpsed at the beginning).
Finally, say that since you memorized the entire red deck, you also know that the selected card is exactly _ cards down in that deck (just say the card’s stack number). Have the spectator holding the red deck remove it from its case and count down (face-up onto the table) that many cards. The card at the named position will match the selection, and both decks are now back in memorized order.
A Pleasant Little Surprise
If you like the bonus routine but would prefer to perform it before “Mathe-match-ics” rather than after, I have good news for you. The “Mathe-match-ics” routine also works if, instead of preparing the red deck by giving it a faro, you prepare the blue deck by giving it an anti-faro. More precisely, the red deck begins in stack order, except with the bottom card (stack #52) on top, and the blue deck is in the anti-faro order 1,3,5,…,51,2,4,6,…,52. As before, card #52 in the blue deck has a bottom-cutting breather crimp. The “Mathe-match-ics” trick will still work exactly as described. To reset the blue deck at the end, just give it a single out-faro.
If you don’t care for the bonus routine, you might still prefer the anti-faro setup (which can be done quickly before your performance) if you’d like to use “Routined Mathe-match-ics” as an opener. At the conclusion of the routine, give the blue deck an out-faro and you now have two apparently shuffled decks in memorized order, awaiting further miracles!
Credits
“Arith-mate-ic” can be found in The Collected Works of Alex Elmsley, Vol. 1 by Stephen Minch (pp. 328-330). It uses a 17-card stack and a single deck, and the coincidence involves mates rather than perfect matches, but Elmsley’s trick is based on the same mathematical principle explained here.
Denis Behr’s “Routined Arith-mate-ic” can be found in Handcrafted Card Magic, Vol. 3, and also on the Disc 4 of the Vanishing Inc. DVD set Magic on Tap. Both are highly recommended. Denis’s routine was also published under the name “Mathe-mate-ics” in Steve Beam’s Semi-Automatic Card Tricks, vol. 10. In these sources, Denis also explains an observation, due to Pit Hartling, that the stack required for Elmsley’s original single-deck effect is essentially built in (by accident!) to Juan Tamariz’s Mnemonica stack.
Tomas Blomberg was the one who first suggested to me that one could perform “Routined Arith-mate-ic” using any stack by making use of a second deck. It’s obvious once you think about it (and know how the trick works), but it came as a revelation to me.
The pseudo-memorization “bonus routine” for mem-deck practitioners was inspired in part by Denis Behr’s “A Packet Trick” from Handcrafted Card Magic, Vol. 1.
Coda: Another True Story
I’d like to conclude with another anecdote. As a graduate student at UC Berkeley, I designed and taught a course in business mathematics for inner-city high-school students from San Francisco. We began by covering basic concepts about linear equations and graphing, and I struggled at first to connect with some of the students in the class. For example, when I tried to illustrate the idea of a linear relationship using Celsius to Fahrenheit temperature conversions, one of the students indignantly shouted, “I’m never going to go to Europe, so why should I care about Celsius?”
This made a deep and lasting impression on me. It hadn’t even occurred to me that the “wonderful” example I had come up with in my own mind was not viewed as particularly interesting or relevant by the students. That evening I scrambled to rewrite my syllabus, and in the next class I tried something completely different: I had the students create their own fictitious businesses and then graph profits versus expenditures, etc. The class went much more smoothly from that point on: the idea of owning a business was something truly meaningful for them.
This experience made a lasting impressing on the magician in me as well. Too often we view magic through our own eyes rather than through the eyes of our audiences. Never forget that it’s the audience, not you, who decides if a trick is interesting and meaningful!
Back to blog homepage
Similar posts on the blog:
