Location. Location. Location.
By Matt Baker - Wednesday, April 14, 2021
I don’t typically perform or write about card tricks where the main effect is that a chosen card is lost and then found. I suppose the whole genre feels a bit tired to me, and it can be hard to make such tricks feel meaningful. However, there are always exceptions, and this month I’m writing about a delightfully subtle card location based on not one but TWO sophisticated math principles: the S/D Location and Penelope’s Principle. Thanks to Dave Solomon for giving me permission to teach this creation of his. Without further ado, I bring you my own presentation for Dave’s effect, a description of the method, and an explanation for why it works.

Effect
“Do you believe that everything in life happens for a reason? I'm not so sure, myself. But I do know that everything in card magic happens for a reason.” The magician places a deck of cards onto the table. “Here, let me show you.”
“In just a moment, I'm going to have you select a card. And do you know the reason why? Because it's a card trick! Those are the rules.” The magician pushes the deck toward the spectator.
“Please cut off less than half the deck and give the cut-off packet a good shuffle. Take a peek at the card you’ve shuffled to the top of your packet and remember it. I'll turn my head as you do that… do you know why? Because if I see your card, this whole trick is really dumb.” The spectator does as instructed while the magician’s head is turned.
“Please cut off a good chunk of the cards remaining on the table and place them on top of the cards in your hand, burying your selection somewhere in the middle. Now I think you’d have to agree, there’s no way I could know at this point either what or where your card is. And in the world of card magic that's a good thing -- it makes the trick much more interesting! Just to be sure, though, give the packet in your hands a cut. Your card is obviously lost now, so I'll turn back around.” The magician takes the packet back from the spectator.
“Now, I asked you to give the packet a cut [the magician demonstrates by giving it a cut himself], and I'm sure there was a reason you cut exactly where you did. You may not know why, and I may not know why, but there must have been a reason for it. I also asked you to shuffle the cards, but I didn't tell you how to shuffle. Most people would do an overhand shuffle, like this [the magician demonstrates]. But I don't know if that's what you did… Maybe you're a card sharp and you did an in-the-hands weave shuffle, like this [the magician demonstrates once again]. Or maybe it was some other kind of shuffle altogether. All we know is that, however you shuffled the cards, it must have happened that way for a reason.”
“You made another decision as well, though I'll bet you didn't even realize you were making it. Through your various actions, you left a specific number of cards on the table. And I don't believe it was a random choice — I think it was in fact a subconscious prediction on your part.
I think you were predicting the exact position where your chosen card would end up in this packet.” The magician places the packet in his hands down onto the table.
“Now so far, no one — not you, and not even me — knows your predicted number. Well, now is the moment of truth: please go ahead and count.” The spectator counts the cards which were left on the table and announces the result (let’s say it’s 17). “Interesting... whether consciously or not, you left exactly 17 cards on the table. So let's count down 17 cards…” The magician counts to the 17th card in the shuffled packet and then pauses. “This is card #17, yes? For the first time, what card are you thinking of?” The participant says (for example) the Queen of Spades.
“Well, I'm not sure why most things in life happen the way they do, but I know that one of the main reasons I do card magic is because of how much I love this moment…”
The magician turns over card #17. It’s the Queen of Spades.
Method:
You’ll need a complete deck of 52 cards, and you’ll need to be able to do a faro shuffle. To set up, place a bottom-cutting reverse breather crimp in the 26th card from the top.
Walk the participant through the procedure for selecting a card, as described above. (In the first part of the procedure, the participant should cut off less than half the deck, and preferably more than a quarter.) After the participant buries his selected card and gives the packet a cut, take the packet back from him.
The first thing you need to do is cut the breather crimp to the bottom. Next, give the packet an Ireland-style overhand shuffle: chop off a block of a few cards, then run about 13 cards singly, then shuffle off the rest. Finally, cut the packet into approximately two equal parts and give it a faro shuffle. The original bottom card should stay on the bottom, and while the faro need not be perfect, it does need to be mostly perfect from the bottom up. (I’ll explain in more detail below what I mean by “mostly perfect”.)
That’s it — everything else simply works because of the mathematics involved. Go ahead, give it a try. Unless you’re already familiar with the underlying math (in which case maybe you should be writing this blog!), I bet you’ll fool yourself, despite the fact that I just “explained” the method. That’s what’s so great about this particular combination of principles…
Explanation
We now come to the meat & potatoes of the post: figuring out why the trick works. It will be convenient to break the explanation into two parts: the S/D Location and Penelope’s Principle.
The S/D Location
The S/D Location is based on the old concept of a “floating key”, but in the present form it’s due to Steve Draun and David Solomon (hence the S/D). The result of the S/D Location procedure is that once the magician cuts the breather crimped card to the bottom of the packet, the selection will be exactly 26 cards from the bottom of the deck.
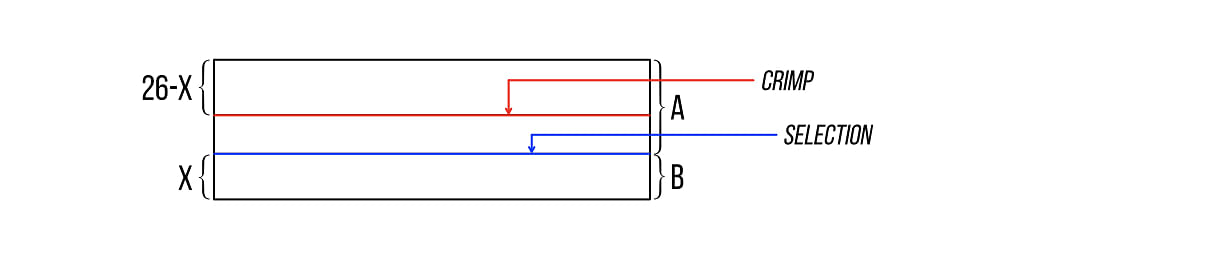
Here’s why it works. Let’s say that the participant initially cuts off X cards and shuffles them. He then peeks at the new top card (which we’ll refer to as the selection) of the shuffled packet (which we’ll refer to as Packet B). Since we’re requiring that X is less than 26, the breather crimp (which begins at position 26) will not be among the cards which get shuffled. However, since the participant is asked to cut off “a good chunk of the remaining cards” and place them on top of the selection, the second cut-off packet (which we’ll call Packet A) will contain the breather.
Before the spectator cuts the cards, here’s what the combined packet looks like:
After the magician cuts the breather crimp to the bottom, the packet looks like this:
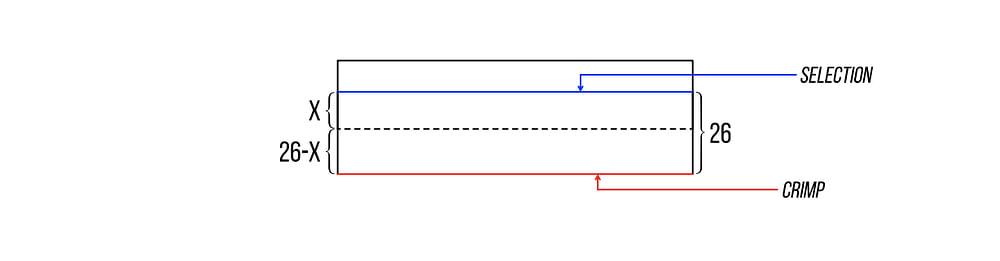
So the selection is now located X + (26 - X)= 26 cards from the bottom of the packet.
Interlude: The Ireland Shuffle
After the Ireland shuffle, instead of being 26 cards from the bottom of the packet, the selection will be 26 cards from the top. We leave it as an exercise to the reader to figure out why. (Yes, I’m a mathematician!)
Penelope’s Principle
Penelope’s Principle is a marvelous discovery due to Alex Elmsley. In the present context, the principle asserts:
If the selection begins 26 cards from the top of a packet consisting of 52 - Y cards, then after a “nearly perfect” bottom out-faro, the selection will be Y cards from the top.
To see why this works (and to give a precise meaning to “nearly perfect”), let’s analyze what happens when we split the packet into two approximately equal halves and then weave the two halves together (with the bottom card staying on the bottom). Let’s call the top half Packet C and the bottom half Packet D.
For the math to work out right, we need the selection to end up in Packet D. (More on this assumption in a moment…)
By assumption, since the selection begins 26 cards from the top and there are 52 - Y cards in the whole packet, there are 26 - Y cards below the selection in Packet D. After a bottom out-faro, this number doubles, so there are now 2(26 - Y) = 52 - 2Y cards below the selection in the shuffled packet. Since the packet has 52 - Y cards in total, the selection is now (52 - Y) - (52 - 2Y) = Y cards from the top, as claimed.
Finally, what do we mean by “nearly perfect”? Well, this means two things:
The selection should end up in Packet D. This will automatically be the case unless the top half contains significantly more cards (roughly Y/2) than the bottom half. If you’re at all worried about this, just make sure when you split the cards in preparation for the faro shuffle that the bottom half is at least as big as the top half. Then it will work 100% of the time.
The faro weave itself should be perfect from the bottom of the packet up to the selection. Once you get above the selection, it doesn’t matter. To be safe, I always try to ensure that the smaller of the two packets weaves perfectly into the larger one. However, it’s nice to know that a small mistake at the end of the shuffle will typically not make a difference.
Credits and Further References
The trick I’ve taught in this post (sans the presentation) is called “Smaltzy Penelope”, and can be found on pp. 142-143 of David Solomon’s terrific book Solomon’s Secrets (Squash Publishing, 2018). The title of Solomon’s routine refers to Ed Marlo’s “Smaltzy Showman’s Prediction”, from his Unexpected Card Book, and Alex Elmsley’s “Penelope’s Principle”, from Stephen Minch’s The Collected Works of Alex Elmsley, Vol. 2.
The S/D Location, which is attributed to Steve Draun and David Solomon, was first published in Kabbala (Vol. 1, No. 8, April, 1972). It is also discussed in Eugene Burger’s book Solomon’s Mind (pp. 137-140). There are two excellent routines (“Dead Reckoning” and “Dawn Patrol”) using the S/D location in John Bannon’s book Dear Mr. Fantasy.
In addition to several routines by Elmsley himself in The Collected Works of Alex Elmsley, Vol. 2, there are a number of other published routines which make use of Penelope’s Principle. My personal favorites include Woody Aragon’s “Maverick” (A Book in English, pp. 131-138), Luis Otero’s “Penelope Does It Herself”, and R. Paul Wilson’s “Con Cam Rendezvous”. While most Penelope-based routines require a faro shuffle, a notable exception is Mike Powers’s “Numerical Analysis” (Power Plays, pp. 106-107), which is completely self-working. For other routines using Penelope’s Principle, see the Conjuring Archive.
If you’re wondering why it’s called “Penelope’s Principle”, here’s what Stephen Minch says about the matter on p. 313 of The Collected Works of Alex Elmsley, Vol. 2: “Penelope was the daughter of Icarius and the fabulously faithful wife of Odysseus, who, during Odysseus' twenty-year absence, wove and at night unwove a tapestry, at the completion of which she had vowed to make a choice from importuning suitors. Mr. Elmsley's unending tapestry is the woven deck.” So there you have it.
Back to blog homepage
Similar posts on the blog:
