History Of The Tower Of Hanoi Problem
Puzzles and mathematics have always shared a harmonious relationship. In fact, mathematical concepts are the core theme behind many of our favorites games, puzzles and riddles such as tic-tac-toe, chess, sudoku and nonograms. However, one logic problem that truly unites everyone from puzzle lovers to math geeks is the Tower of Hanoi.

What is Tower of Hanoi?
While you might not immediately recognize the name, many of you will probably recognize the Tower of Hanoi as soon as you see it. The Towers of Hanoi, also called Tower of Brahma, Lucas’ Tower, or more simply, the pyramid puzzle, is a mathematical game using three rods and various numbers of colored disks stacked in descending order with the larger disk on the bottom and the smaller disks stacked on top. This creates the iconic cylinder or pyramid shape that the Tower of Hanoi is known for.
The object of the Tower of Hanoi puzzle is to move all the disks from the left rod to the right rod. However, while this seems simple at first, there are a few rules that make this classic puzzle game such a favorite among puzzlers and math teachers alike:
- Only one disk may be moved at a time
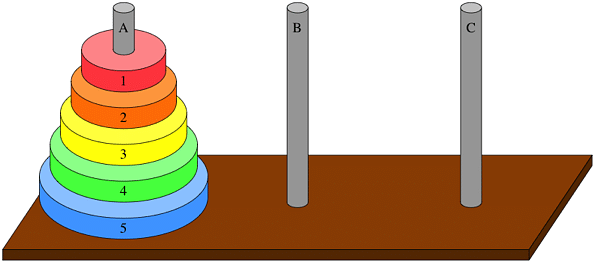
- You can only move the disk that is on top of a stack
- Each disk can be placed on any rod, but it cannot be placed on top of a smaller disk
The Tower of Hanoi can be played with any number of disks. However, most toy versions come with anywhere from 5 to 9 disks.
History of Tower of Hanoi
Since the Tower of Hanoi puzzle was first introduced by French mathematician Édouard Lucas in 1883 (hence the name Lucas Tower), many myths about its origins have been shared. The most popular one is the mystical theory that it is an homage to an ancient Indian temple in Kashi Vishwanath where Brahmin priests have been acting out an ancient prophecy since the beginning of history (this is where the name Tower of Brahma came from).
This temple houses a room with three massive pillars wrapped with 64 golden disks. Acting under Brahmin rule, the priests are continually moving the disks, one disk at a time. It is believed that once the Tower of Brahma is complete, the world would end.

However, there probably isn’t reason to panic just yet. One of the best parts about mathematical puzzles is that we can easily calculate how long they would take to solve. If the legend were true, and the priests were also able to find a remarkably efficient way to move one disk per second, it would take an mind-boggling 585 billion years to complete the task. As that is approximately 42 times the current age of the universe, we should be safe for now.
The Tower of Hanoi has also had a prominent role in pop culture and video games. Most notably, in a 1966 episode of Dr. Who where The Doctor was forced to play a mind-numbing 1,023-move Tower of Hanoi puzzle called “The Trilogic Game” and in the 2011 blockbuster movie Rise of the Planet of the Apes where it was used as an intelligence test for the apes.
How to Solve the Tower of Hanoi
While the Tower of Hanoi is rooted in mathematics, you don’t need to understand or use complex math to solve it. In fact, learning how to solve it can be easier than learning card tricks!
Each Tower of Hanoi problem has a minimum number of moves to solve it that is based on the amount of disks you start with. For example, in a 3-disk problem, you will have to use a minimum of 7 moves. Every time you add another starting disk, that minimum number of moves is doubled + 1. So, a 4-disk problem takes 15 moves, a 5-disk problem takes 31 moves, a 6-disk problem takes 63 moves and so on.
If you’re interested in the math behind solving a Tower of Hanoi problem, it works like this. The minimum number of moves required to solve a Tower of Hanoi is 2 to the power of N minus 1 (2n-1). In this case, the “N” represents the amount of starting disks.
There are three main methods for solving Towers of Hanoi puzzles in the fewest amount of moves:
Iterative Solution
 This is a very basic solution using a repeated sequence of instructions until the puzzle is solved. For the Hanoi toy puzzle, this means alternating between the smallest piece and largest available piece (remembering that you can only take from the top of a stack of disks). Each piece is always moved to the next available position in the same direction (left if you start with an odd amount of pieces or right if you start with an even amount).
This is a very basic solution using a repeated sequence of instructions until the puzzle is solved. For the Hanoi toy puzzle, this means alternating between the smallest piece and largest available piece (remembering that you can only take from the top of a stack of disks). Each piece is always moved to the next available position in the same direction (left if you start with an odd amount of pieces or right if you start with an even amount).
If there is no available position in the correct direction, you then would move the piece to the opposite end and continue in the correct direction. For example, your first move in a 3-disk problem should be to move the smallest disk to the left. Since there are no pegs available to the left, you’d bring it around to the opposite side (peg 3). You do the same with the medium sized peg; however, since it can’t be placed on peg 3 (you can’t place a larger disk on top of a smaller disk), you would move it to the next available peg to the left (peg 2). You then move the smallest disk to the left and keep alternating between the smallest and non-smallest disk until you solve the tower.
Recursive Solutions
Some people, particularly scientists and computer programmers, love to explore the idea of recursive solutions for Tower of Hanoi problems. You can spend hours explaining this, so we will try to keep it as simple as possible.
At their core, recursive solutions recognize that a problem can be broken down into a collection of smaller sub-problems. Each of these sub-problems is easier to manage and the sum of their solutions combines to find the total solution for the base case. Simply put, you use the information from one step to inform the next step.
Finding Your Own Patterns
When first presented with a Tower of Hanoi puzzle, this is the strategy most people use. You simply play the game and find your own patterns and solutions as you go. While this isn’t the most effective strategy, it’s definitely the most fun. Even if you fail, you can always just start over. That’s the fun of a game!
If you enjoy Tower of Hanoi, then you should definitely check out our other free brain teasers and riddles that you can show your friends and family. These, along with our other unique puzzles and mindful play toys, are great ways to exercise your brain and keep your mind sharp.
Shop Fun Puzzles
Useful links for our magic products
